Variational Autoencoders for Timeseries Data Generation

An Innovative Approach to Generating Synthetic Timeseries Data through VAEs

Variational Autoencoders (VAEs) have emerged as a powerful tool in machine learning, particularly for generating new data from learned representations. In this post, we will explore a practical implementation of a VAE designed specifically for generating synthetic timeseries data. By the end, you will have a good understanding of the code and how it works.

What is a Variational Autoencoder?

A Variational Autoencoder is a type of generative model that learns to represent data in a lower-dimensional latent space. The VAE consists of two main components: the encoder, which compresses the input data into a latent representation, and the decoder, which reconstructs the original data from this representation. Unlike traditional autoencoders, VAEs assume that the latent space follows a probability distribution, usually Gaussian. This allows VAEs to generate new data by sampling from this distribution, making them particularly useful for tasks like anomaly detection, data generation, and unsupervised learning.

Photo by Chris Liverani on Unsplash

Key Features of the VAE:

• Generative Capability: VAEs can generate new data samples by sampling from the latent space.

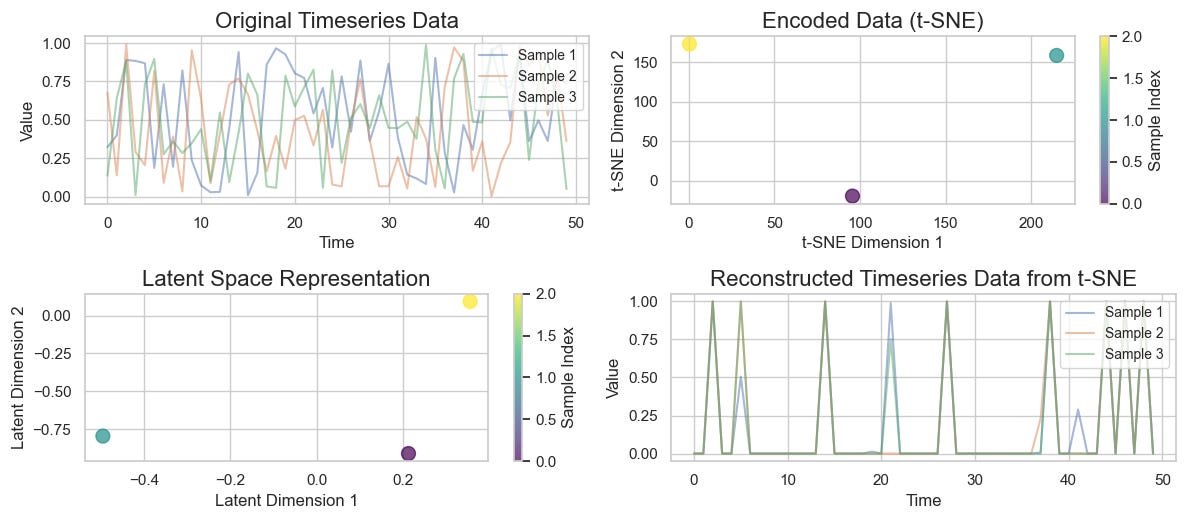
• Latent Space Representation: The structure of the latent space reveals patterns in the data.

Why Use VAEs for Time Series?

Time series data—such as stock prices, weather patterns, or even EEG signals—often requires specialized methods due to its temporal nature. By leveraging VAEs, we can capture the underlying patterns of time series data in a compressed form. This can help us visualize the data more effectively, reduce dimensionality, and even generate new synthetic time series that resemble the original dataset.

Our Approach

In this implementation, we generate synthetic time series data, train a VAE to learn latent representations, and use t-SNE (t-distributed Stochastic Neighbor Embedding) to visualize the lower-dimensional embeddings. We’ll also reconstruct the data to see how well the VAE performs in recreating the original time series.

Explanation of Key Components

1. Data Generation: The generate_timeseries_data function creates synthetic timeseries data for training the VAE. It generates random values within a specified shape.

def generate_timeseries_data(num_samples, num_timesteps):
    """
    Generate synthetic timeseries data.

    Parameters:
        num_samples (int): Number of samples in the dataset.
        num_timesteps (int): Number of timesteps in each sample.

    Returns:
        np.ndarray: Generated timeseries data with shape (num_samples, num_timesteps).
    """
    return np.random.rand(num_samples, num_timesteps)

2. VAE Class: The VAE class encapsulates the architecture of the autoencoder:

• Encoder: Maps the input data to a latent space using a dense layer.

• Decoder: Reconstructs the input data from the latent representation.

  class VAE(models.Model):
      """
      Variational Autoencoder (VAE) model.
  
      Parameters:
          input_dim (int): Dimension of input timeseries data.
          latent_dim (int): Dimension of the latent space.
      """
  
      def __init__(self, input_dim, latent_dim):
          super(VAE, self).__init__()
          self.input_dim = input_dim
          self.latent_dim = latent_dim
  
          self.encoder = self.build_encoder()
          self.decoder = self.build_decoder()
  
      def build_encoder(self):
          encoder_input = layers.Input(shape=(self.input_dim,))
          x = layers.Dense(128, activation='relu')(encoder_input)
          z_mean = layers.Dense(self.latent_dim)(x)
          z_log_var = layers.Dense(self.latent_dim)(x)
          encoder_output = layers.Lambda(self.sample_z, output_shape=(self.latent_dim,))([z_mean, z_log_var])
          return models.Model(encoder_input, [z_mean, z_log_var, encoder_output])  # Ensure to return all three outputs
  
      def build_decoder(self):
          decoder_input = layers.Input(shape=(self.latent_dim,))
          x = layers.Dense(128, activation='relu')(decoder_input)
          decoder_output = layers.Dense(self.input_dim, activation='sigmoid')(x)
          return models.Model(decoder_input, decoder_output)
  
      def sample_z(self, args):
          z_mean, z_log_var = args
          batch_size = tf.shape(z_mean)[0]
          latent_dim = tf.shape(z_mean)[1]
          epsilon = tf.random.normal(shape=(batch_size, latent_dim), mean=0., stddev=1.0)
          return z_mean + tf.exp(0.5 * z_log_var) * epsilon
  
      def call(self, inputs):
          z_mean, z_log_var, z = self.encoder(inputs)  # Correctly unpack all three outputs
          reconstructions = self.decoder(z)
          return reconstructions, z_mean, z_log_var

  3. Loss Function: The vae_loss function combines reconstruction loss and Kullback-Leibler (KL) divergence to ensure the model learns a smooth latent space.

  def vae_loss(y_true, y_pred, z_mean, z_log_var):
      """
      Define the loss function for the VAE model.
  
      Parameters:
          y_true (tf.Tensor): Ground truth values.
          y_pred (tf.Tensor): Predicted values (reconstructed data).
          z_mean (tf.Tensor): Mean of the latent variable.
          z_log_var (tf.Tensor): Log variance of the latent variable.
  
      Returns:
          tf.Tensor: Total loss (reconstruction loss + KL divergence).
      """
      mse_loss = tf.keras.losses.MeanSquaredError()
      recon_loss = mse_loss(y_true, y_pred)
      kl_loss = -0.5 * tf.reduce_mean(1 + z_log_var - tf.square(z_mean) - tf.exp(z_log_var))
      return recon_loss + kl_loss
  

  4. Training Loop: The main function handles the data normalization and training process of the VAE over specified epochs.

  def main(num_samples, num_timesteps, latent_dim, epochs, batch_size):
      # Generate synthetic timeseries data
      data = generate_timeseries_data(num_samples, num_timesteps)
  
      # Normalize the data
      data_mean = data.mean()
      data_std = data.std()
      data_normalized = (data - data_mean) / data_std
  
      # Create VAE model
      vae = VAE(num_timesteps, latent_dim)
      vae.compile(optimizer='adam')  # Remove the custom loss from here
  
      # Custom training loop
      for epoch in range(epochs):
          with tf.GradientTape() as tape:
              reconstructions, z_mean, z_log_var = vae(data_normalized)
              loss = vae_loss(data_normalized, reconstructions, z_mean, z_log_var)  # Pass the outputs to the loss function
          
          grads = tape.gradient(loss, vae.trainable_variables)
          vae.optimizer.apply_gradients(zip(grads, vae.trainable_variables))
  
          print(f'Epoch {epoch + 1}, Loss: {loss.numpy()}')  # Print the loss for each epoch
  
      # Reduce dimensionality of timeseries using the trained encoder
      z_mean, z_log_var, encoded_data = vae.encoder.predict(data_normalized)

  5. Visualizations: After training, we visualize the original timeseries data, the encoded data in the latent space, and the reconstructed data.

The code generates several visualizations:

• Original Timeseries Data: Displays the input data.

• Encoded Data (t-SNE): Shows the latent representation reduced to 2D.

• Latent Space Representation: Visualizes the encoded data in the latent space.

• Reconstructed Timeseries Data: Illustrates how well the model can reconstruct the original data.

Conclusion

VAEs are a powerful way to understand and generate timeseries data, providing insights into the underlying patterns within the data. By utilizing TensorFlow and Keras, this implementation offers a flexible and robust framework for experimentation.

For the complete code and further exploration, check out the GitHub repository.